Reduced Order Multirate Schemes

Building on the previous blog entry we will continue discussing the combination of model order reduction (MOR) and Multirate (MR) time integration, called the reduced order multirate (ROMR) method.

In this post we’ll explore the effectiveness of the ROMR method by applying it to an example circuit. Hence, consider the circuit depicted in Figure 1. This circuit consists of an operational amplifier, two resistors, a diode and a capacitor. The resistor R(T) produces and transports heat and is temperature dependent. The amplifier is a heat source

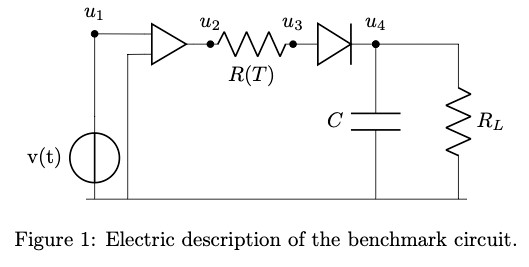
and the diode has a temperature dependent characteristic curve. Now this system can be naturally partitioned into a slow and fast subsystem by grouping together the electrical equations in a fast subsystem and the discretized thermal equations in a slower subsystem. Furthermore, the large nonlinear thermal subsystem is reduced by a reductive projection matrix, V. The system can then be mathematically described by

where the overdots denote time derivatives, the subscripts F, S stand for the fast and slow timescales and R indicates the reduced state vector of the slow subsystem. In Figure 2 the results of a transient analysis are shown, in which you can see the different time-scales in action.

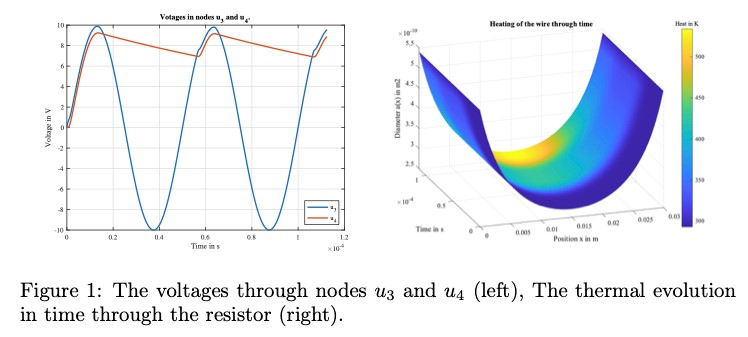
To assess the performance of the ROMR scheme the obtained voltages at nodes u 3 and u 4 are compared to a highly accurate reference solution. Figure 3 shows this comparison for the single rate ( scheme, the MR scheme and the ROMR scheme. It shows that the reduced order multirate scheme error, the left figure, follows the O(H) convergence rate. In the right figure, it shows the computation time versus the difference with the

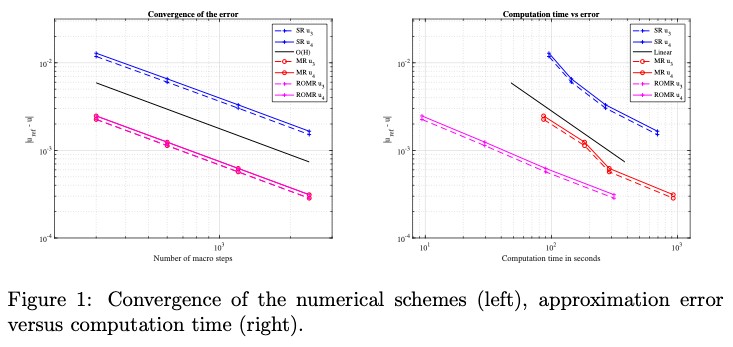
reference solution. From these figures we see that the ROMR scheme decreases the computation time whilst maintaining the MR accuracy. I hope you enjoyed this instalment of our ROMSOC blog. To follow the progress of my fellow researchers and I please keep an eye on the ROMSOC website and follow us on Twitter and Facebook!

For now servus and a rrivederci
Marcus Bannenberg

About the author

Marcus Bannenberg is an early stage researcher ( in the Reduced Order Modeling Simulation Optimization and Coupled methods ( project. He is a PhD student at the Bergische Universität Wuppertal and working in collaboration with STMicroelectronics. His research project is focus ed in numerical analysis/applied mathematics on the combination of model order reduction and multirate techniques.