The significant contributions and problems posed by the peers over time have all contributed to the development of scientific knowledge. Being curious about the history of scientific evolution can generally help develop a new organic perspective. It provides an invaluable lesson by leading us through the reasoning and choices along the path of scientific progress. The last couple blog posts ( viz., Origin and need for coupled models in acoustics – ROMSOC and Mathematical modelling acoustic measurements – ROMSOC ) have shed light into the motivation and approach followed in coupled systems modelling in acoustic industry, while this post intends to delve deep into the world of modeling acoustics in fluid flow. Describing fluid flow models while also coupled with acoustics is definitely harder in ‘simpler’ terms, I assume the reader is somewhat familiar to fluid flow models.
Almost always, fluid flow in mathematical models begins with the Navier-Stokes(NS) equations and involves some reformulation/restructuring, simplification along with/without change in frame of reference. Lighthill and Curle (1950-60s) pioneered the development in this regard especially in the field of aeroacoustics providing models for jet noise prediction with a rearranged NS equation in the form of a linear wave equation for a fluid medium at rest. The model primarily assumes a equivalent-source analogy- suggesting that the source term may always be modeled approximately. Subsequent works by Ffowcs Williams, Hawkings, Phillips and Liley extended this approach by restructuring the NS equations into a more general form of convective wave equation. These models could help predict sound generation in simple geometries and flow profiles, but complex cases required by the industry were still out of reach. A multitude of empirical and semi-empirical approaches for specific applications followed, although failing to address a holistic analogy for flow acoustics.
Another favored modelling approach was to make some simplifications on the much harsher NS equation and trying to tame a simpler set of equations hoping that they cater to the complex cases. Euler equations for one, are simplified NS equations with the effects of viscosity and heat transfer omitted. Convenient linear approximations on density, pressure and velocity fields around the mean flow give the Linearized Euler Equations (ironically since the equations themselves are non-linear). These equations received interest especially in fluid-structure interaction problems since they could capture refractional effects and reflections at solid boundaries (especially relevant for aero-industry); however, they are often used for 2D geometries and behave well only for low amplitude acoustic perturbations. The model is still sensitive to small changes and there are further simplified LEE models e.g. Bogey-Bailly-Juve model which ignores some more terms to make the model simpler.
I would like to shed light into one of the less-known models – the Galbrun’s equation. This less-used model utilizes a different form of the NS equations within a mixed frame of reference. It assumes a known stationary underlying Eulerian flow and models the Lagrangian fluctuations of acoustics. The displacement formulation of it is given as,
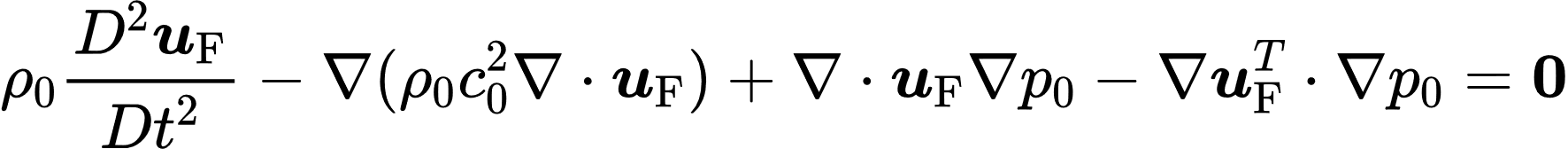
Here, and are the density and speed of sound of the underlying flow with a pressure field while, is the material derivative. The model offers advantages in coupling problems, especially the compatibility of boundary conditions using Lagrangian terms, and offers an option to modularize the problems of fluid flow and the acoustic fluctuations. It also comes with a few setbacks – the equation is notoriously unstable with traditional finite elements and needs ‘regularization’ for effective use as was demonstrated by Bonnet-Ben Dhia and others [REFs]. Addressing these challenges could provide for a powerful tool to integrate acoustics in flowing medium, helping develop better noise predictions in fluid flow and the ROMSOC project hopes to address this for the real-world applications by providing the open-access knowledge and tools. Keep following this blog for more information into a diverse set of mathematical technologies that ROMSOC hopes to develop for industry.
References:
Howe, M. (1998). Acoustics of Fluid-Structure Interactions (Cambridge Monographs on Mechanics). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511662898
Goldstein, M. E. (2003). A generalized acoustic analogy. Journal of Fluid Mechanics, 488, 315–333. https://doi.org/10.1017/S0022112003004890
Billson, M., Eriksson, L.-E., & Davidson, L. (2005). Acoustic Source Terms for the Linearized Euler Equations in Conservative Form. AIAA Journal, 43(4), 752–759. https://doi.org/10.2514/1.12858
Maeder, M. (2020). 90 Years of Galbrun’s Equation: An Unusual Formulation for Aeroacoustics and Hydroacoustics in Terms of the Lagrangian Displacement. 39.
About the author:
Ashwin Nayak is an early-stage researcher (ESR2) in the Reduced Order Modeling Simulation Optimization and Coupled methods (ROMSOC) project. He is affiliated with the Technological Institute of Industrial Mathematics (ITMATI), Spain and working in collaboration with Microflown Technologies B.V., Netherlands. His research aims to develop coupled mathematical models to enable acoustical measurements in fluid-porous media interactions.